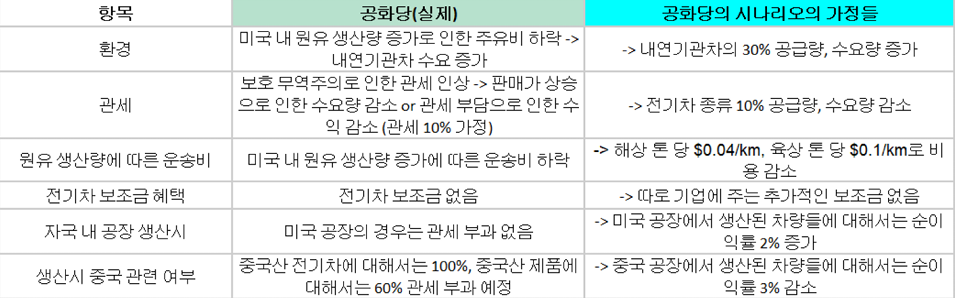
2024년 kaist에서 진행한 IE Field camp에서 수행했던 과제를 기록하고자 작성합니다.
주제는 2가지로, 첫 번째는 시뮬레이션 프로그램을 통한 지하철 개찰구 최적화, 2번째는 대선결과에 따른 현대자동차 전략수립입니다.
저희 조는 2번주제를 맡아 미국 대선별 각 산업별 영향과 현대자동차의 전략, 수송계획법에 대해서 설명하겠습니다.

2번 주제는 총 2개의 세션으로 이루어져 있으며 Session1 은 대선별 영향분석이고, Session2는 대선결과에 따라 임의로 부여한 조건에 따라서 수송계획 문제를 푸는 형태입니다.
목차에는 안나와 있지만 SESSION1, 2 모두 2개의 Task로 이루어져 있습니다.
<SESSION1>
1-1 TASK1: 미국 대선 결과에 따른 '반도체', '자동차', '이차전지' 산업군의 영향 분석
조건: 원자재 수요, 부품 및 제조, 기술 및 연구 개발, 생산, 유통 및 판매 측에서 제시
-반도체 sector
1. 원자재 수요
| 공화당- 트럼프 | 민주당- 해리스, 바이든 |
| 1. 중국과의 무역갈등 심화(디커플, 비동조화) -> 희토류 등 원자자재 수급의 어려움이 예상 -> 최종 소비자 제품 가격 상승 2. 자국 우선주의에 따른 미국 내수강화 -> 미국 내 반도체 산업의 발달 |
1. 기후변화 대응 및 친환경 정책 추진으로 인한 친환경 투자증가 -> 관련 원자재 수요 증가 2. 국제 협력을 통한 원자재 수급의 안정성 확보 노력 지속 |
2. 부품 및 제조
| 공화당- 트럼프 | 민주당- 해리스, 바이든 |
| 1. 제조업의 미국 회귀를 추진하는 리쇼어링 정책 -> 국내 제조업체들의 비용 상승 예상 2. 중국산 부품에 대한 관세 인상으로 인한 부품수급 문제 -> 한국 제조사들의 반도체 생산 차질, 공급망 다변화 필요성 증대 |
1. 친환경 기술 개발 및 적용을 추진, 자국 내 생산강화 -> 관련 부품 수요증가 2. 국제 무역 협력 강화 -> 부품 수급 원활 |
3. 기술 및 연구개발
| 공화당- 트럼프 | 민주당- 해리스, 바이든 |
| 칩4와 같은 바이든 정부의 정책을 폐기할 가능성, 자국의 기술독립을 강조 -> 자국 반도체 산업에 대한 보조금 확대 -> 미국 내 반도체 산업 활성화 |
1.택사스 중부 첨단 반도체 산업 생태계 구축, 삼성전자와 의 예비 조건 발표 -> 한국 반도체 산업의 기대효과 2. 바이든 정부의 반도체 지원법에 따른 연구개발 투자증가 -> 미국 내 반도체 산업 활성화 |
칩스법: 자국 내 반도체 시설투자에 대해 세액공제율을 적용하는 것
4. 생산
| 공화당- 트럼프 | 민주당- 해리스, 바이든 |
| 1. 미국 내 반도체 생산 강화로 인한 환경, 노동 규제 완화 -> 미국 내 제조업 일차리 창출 -> 생산비용 절감, 생산성 향상 2. 자국 내 생산을 강조하면서 절세 등 혜택 강화 -> 반도체 생산 확대 3. 중국과의 무역 갈등 -> 원자재 및 부품 수급 문제 발생 |
1.미국 내 글로벌기업의 반도체공장 증설 -> 생산 효율성 증대 2. 국제 협력 정책 -> 안정적인 생산 환경 조성 3. 신재생에너지 대체로 인한 전기요금 상승 -> 반도체 생산비용 증가 |
5. 유통 및 판매
| 공화당- 트럼프 | 민주당- 해리스, 바이든 |
| 1.보호무역주의 정책으로 -> 미국 내 판매 경쟁 증가 2. 중국과의 무역갈등 -> 공급망의 다변화 발생 |
1.친환경 제품에 대한 수요 증가 -> 새로운 시장 형서 가능 2. 자유무역협정 강화 -> 글로벌 유통망 활성화 |
-자동차 Sector
1. 원자재 수요
| 공화당- 트럼프 | 민주당- 해리스, 바이든 |
| 1.철강, 알루미늄 등 자동차 생산에 필요한 관세 인상예상 -> 미국의 해외 원자재 의존도 감소 2. 화석연료의 중요성 증대 -> 미국에 공장이 있는 내연기관 매출 증가 3. IRA 감축으로 인한 배터리 원자재 가격 상승 -> 전기차 순이익률 감소 |
1.친환경 차량 생산을 위해 리튬, 코발트 등 원자재 수요증가 2. 국제 협력을 통해 안정적인 원자재 공급망 구축 -> 원자재 수급 원활 |
2. 부품 및 제조
| 공화당- 트럼프 | 민주당- 해리스, 바이든 |
| 1.미국 내 제조업체에 대한 세제 혜택을 강화 -> 미국 공장 증설, 일자리 창출 2. 해외 자동차 제조사의 보조금을 폐지 -> 해외 제조사의 미국 본토 공장 증성 -> 새로운 일자리 창출 |
1.친환경 정책을 유지함에 따라 각종 친환경 교통수단 개발 2. 전기차가 내연기관보다 수리의 노동력이 적음 -> 수리, 부품업계의 일자리 감소 예상 |
3. 기술 및 연구개발
| 공화당- 트럼프 | 민주당- 해리스, 바이든 |
| 1. 오일에너지 최대생산국으로 전환 -> 전기차보다는 내연기관, 하이브리드 차량에 대한 연구, 개발 증가 2. 외국인 인재 유입 제한 정책 -> 개발 인력 부족문제 발생 |
1. 친환경 기술 개발의 중요성 증가 -> 전기차, 수소차 등의 친환경 차량에 대한 연구, 개발 증가 2. 국제 협력을 통한 글로벌 프로젝트 활성화 -> 생산 공정 효율성증대, 부품의 품질과 성능 개선 |
4. 생산
| 공화당- 트럼프 | 민주당- 해리스, 바이든 |
| 1. 미국 내 생산 촉진 -> 미국 생산량 증가, 생산과정에서 원자재 수급문제 2. IRA에 대한 지원 감축 또는 폐지 -> 아직 경쟁력이 없는 미국 다수 자동차 기업들의 위기 발생 -> 미국 전기차 시장이 테슬라 중심으로 재편 가능성 증가 |
1.국제 협력을 통한 안정적인 생산 환경 조성 -> 생산 효율성 증대 2. 텍사스 반도체 공장 증설로 인한 전기차 생산비용 감소 -> 전기차 순이익률 증가 |
5. 유통 및 판매
| -2차 전지 | |
-이차전지 Sector
1. 원자재 수요
| 공화당- 트럼프 | 민주당- 해리스, 바이든 |
| 1. 무역갈등으로 인해 중국에서 수입했던 배터리 원자재 수급 차질 -> 자국 내 자원개발 촉진 및 해외 원자재 의존도 감소 |
1.친환경 차량 생산을 위해 리튬, 코발트 등 원자재 수요증가 2. 해외 의존도를 줄이기 위한 국내 자원 개발 및 대체 원료 사용 측진 |
2. 부품 및 제조
| 공화당- 트럼프 | 민주당- 해리스, 바이든 |
| 1.미국 내 제조업체에 대한 세제 혜택을 강화 -> 자국 내 부품 개발 촉진 2. 중국 부품에 대한 의존도 낮추기(디커플링) -> 자국내 생산 증가 |
1.친환경 정책을 유지함에 따라 각종 친환경 교통수단 개발 2. 바이든 정부의 IRA도입 -> 일정 비율 이상을 미국내에서 제조야함, 배터리 원자재도 일정부분 북미산 필수 사용 -> 배터리 원자재 대부분을 중국이 독점하고 있어 여러 개업이 타격을 받을 수 있음 |
3. 기술 및 연구개발
| 공화당- 트럼프 | 민주당- 해리스, 바이든 |
| 1. 전기차 배터리 기술개발에 대한 투자 축소 -> 내연기관, 하이브리드 차량에 대한 연구, 개발 증가 2. IRA 축소 및 폐지 -> 이차전지 성장 둔화 예상 |
1. 친환경 차량의 수요증가에 따른 배터리 수요 증가 -> 이차전지의 연구 및 개발 활성화 2. 미국 자국 내 생산 중요성 두각 -> 미국 내 이차전지 연구투자비용 증가 |
4. 생산
| 공화당- 트럼프 | 민주당- 해리스, 바이든 |
| 1. 미국의 자국 생산 정책 -> 회사입장에서는 생산비용 증가 2. IRA에 대한 지원 감축 또는 폐지 -> 이차전지 산업의 생산 중단 위험 |
1. 친환경 생산 공정 도입 -> 생산비용의 증가 가능성 2. 전기 교통수단의 인프라 증가 -> 이차산업의 수요량증가 |
5. 유통 및 판매
| 공화당- 트럼프 | 민주당- 해리스, 바이든 |
| 1.전기차 시장의 정체 -> 이차전지 시장의 캐즘(chasm)현상 발생 |
1. 자유무역 협정의 강화 -> 글로벌 유통망 활성화 2. IRA정책의 이차전지 핵심부품 할당제 -> 중국외의 다른 대체 공급망 마련 필요 |
1-2 TASK2: 대선결과에 따른 현대자동차의 SWOT 분석
조건: 환경, 타 기업과의 협력, 중국과의 관, 자율 전략을 포함


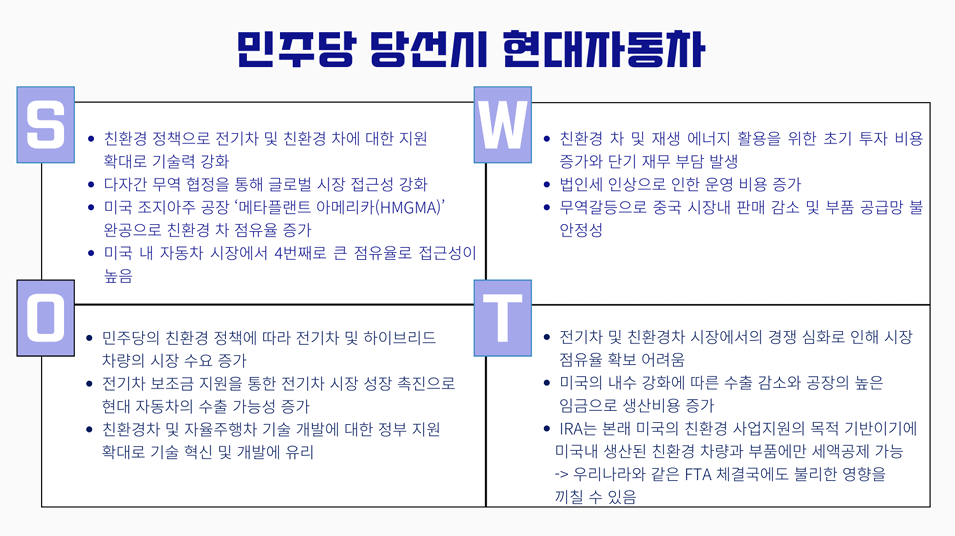

<SESSION2>
2-1 TASK1: 미 대선의 시나리오별(민주당, 공화당) 현대자동차의 수송계획법을 통해 기업의 순수익 계산
조건: 주어진 조건에 따라서 각 순수익을 계산하고 현대자동차에게 더 큰 이득을 주는 대선결과 도출
시퀀스 계산:
- 위도, 경도 수송비용 기준 데이터셋을 이용해서 최적의 루트들을 결정해 수송 비용들을 결정
- 수송계획법을 이용해서 최적화된 목적함수를 구하기(공급지, 수요지등 데이터셋 이용)
- 최적화된 목적함숫값들, 차량의 정보 데이터셋을 이용해서 기업이 얻을 수 있는 순이익 계산
- 위 과정을 이용해서 공화당, 민주당 시나리오를 적용한 최종적인 결과 값들을 도출
1. 기본문제
1-1. 수송비용 구하기

haversine 함수를 통해서 생산공장에서 항구, 항구에서 수요지까지의 직선거리를 구한 뒤 해당 경로에 따라 수송 비용을 곱하여 전체 수송 비용을 출력하고, 최솟값만 추출해 테이블로 만들기
import pandas as pd
from haversine import haversine, Unit
from scipy.optimize import linprog
import numpy as np
# 데이터프레임 생성
supply_data = {
"생산 공장": ["HMI", "HAOS", "BHMC", "HMMA", "HMMC", "HMB", "HMMI", "HTBC", "Vietnam", "Korea"],
"위도": [12.9992, 40.7724, 39.9689, 32.3887, 49.6624, -22.6848, -6.404, 31.118, 21.346, 36.7925],
"경도": [79.9906, 30.0244, 116.3194, -86.3544, 18.396, -47.6035, 107.186, 104.184, 105.61, 126.9928]
}
port_data = {
"미국 항구": ["시애틀 항", "로스앤젤레스 항", "휴스턴 항", "찰스턴 항", "뉴욕 뉴저지 항"],
"위도": [47.3622, 33.74, 29.7426, 32.7812, 40.6688],
"경도": [-122.1955, -118.2727, -95.2622, -79.9283, -74.016]
}
demand_data = {
"수요지": ["시카고", "LA", "워싱턴 DC", "미시간", "뉴욕", "캘리포니아", "몬타나", "플로리다"],
"위도": [41.8666, 36.1495, 38.8221, 44.7375, 40.7576, 36.8192, 45.7338, 27.9837],
"경도": [-87.624, -115.249, -77.0575, -85.5944, -73.7811, -119.7898, -108.6091, -81.679]
}
supply_df = pd.DataFrame(supply_data)
port_df = pd.DataFrame(port_data)
demand_df = pd.DataFrame(demand_data)
# 공급지에서 미국 항구로 가는 거리 및 비용 계산
supply_to_port_cost = np.zeros((len(supply_df), len(port_df)))
for i, supply in supply_df.iterrows():
for j, port in port_df.iterrows():
distance = haversine((supply['위도'], supply['경도']), (port['위도'], port['경도']), unit=Unit.KILOMETERS)
cost = 0.05 * distance
supply_to_port_cost[i, j] = cost
supply_to_port_cost_df = pd.DataFrame(supply_to_port_cost, index=supply_df['생산 공장'], columns=port_df['미국 항구'])
# 미국 항구에서 수요지로 가는 거리 및 비용 계산
port_to_demand_cost = np.zeros((len(port_df), len(demand_df)))
for i, port in port_df.iterrows():
for j, demand in demand_df.iterrows():
distance = haversine((port['위도'], port['경도']), (demand['위도'], demand['경도']), unit=Unit.KILOMETERS)
cost = 0.2 * distance
port_to_demand_cost[i, j] = cost
port_to_demand_cost_df = pd.DataFrame(port_to_demand_cost, index=port_df['미국 항구'], columns=demand_df['수요지'])
# 공장에서 수요지까지의 최소 비용 계산
factory_to_demand_cost = np.zeros((len(supply_df), len(demand_df)))
for i, supply in supply_df.iterrows():
for j, demand in demand_df.iterrows():
min_cost = float('inf')
for k, port in port_df.iterrows():
cost = supply_to_port_cost_df.loc[supply['생산 공장'], port['미국 항구']] + port_to_demand_cost_df.loc[port['미국 항구'], demand['수요지']]
if cost < min_cost:
min_cost = cost
factory_to_demand_cost[i, j] = min_cost
factory_to_demand_cost_df = pd.DataFrame(factory_to_demand_cost, index=supply_df['생산 공장'], columns=demand_df['수요지'])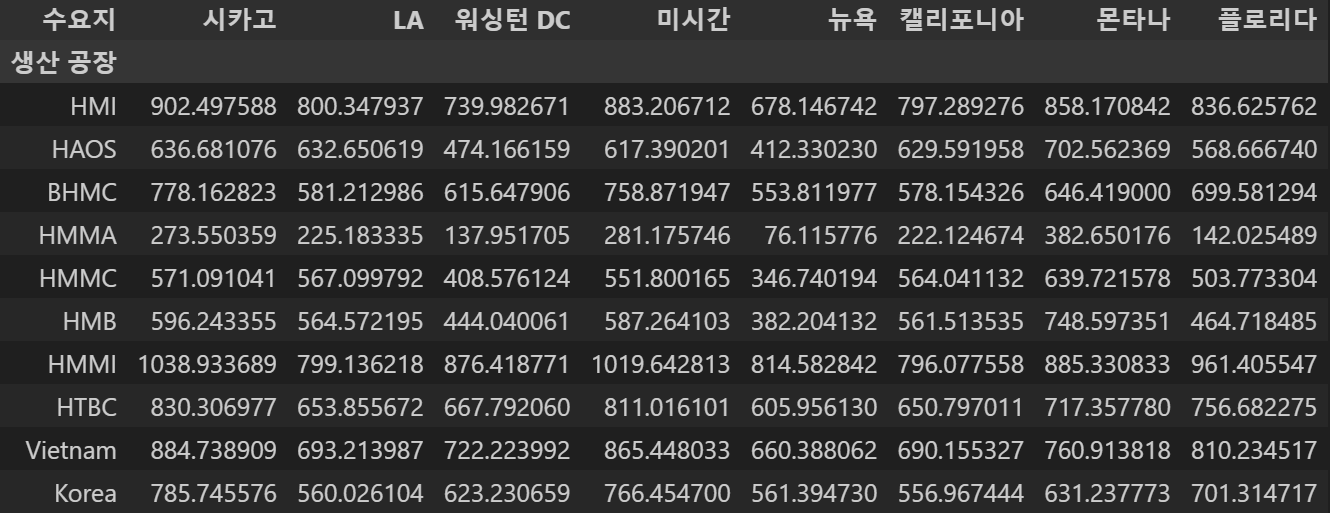
1-2. 각 공급량과 수요량 데이터셋으로 변환하기
# 공급량 데이터
supply = {
("HMI", "Elantra"): 23000, ("HMI", "Sonata"): 8394, ("HMI", "Palisade"): 17019, ("HMI", "Tucson"): 20593,
("HAOS", "Kona"): 22587, ("HAOS", "Venue"): 5973, ("HAOS", "Nexo"): 70,
("BHMC", "Santa Cruz"): 6654, ("BHMC", "Sonata"): 8436, ("BHMC", "IONIQ 5"): 6581, ("BHMC", "IONIQ 6"): 3070,
("HMMA", "Tucson"): 25428, ("HMMA", "Santa-Fe"): 17199, ("HMMA", "GV70"): 4812, ("HMMA", "GV70 EV"): 828,
("HMMC", "Elantra"): 27273, ("HMMC", "Kona"): 17048, ("HMMC", "Tucson"): 32544, ("HMMC", "Palisade"): 17330,
("HMB", "GV60"): 989, ("HMB", "GV70"): 3493, ("HMB", "GV70 EV"): 698, ("HMB", "GV80"): 4248,
("HMMI", "Santa-Fe"): 29620, ("HMMI", "Santa Cruz"): 8322, ("HMMI", "Sonata"): 8382, ("HMMI", "Palisade"): 10195, ("HMMI", "Venue"): 4854,
("HTBC", "G70"): 2769, ("HTBC", "G80 (RG3)"): 788, ("HTBC", "G80 (RG3 EV)"): 124, ("HTBC", "G90"): 206,
("Vietnam", "IONIQ 5"): 8374, ("Vietnam", "IONIQ 5 Robo Taxi"): 18, ("Vietnam", "IONIQ 6"): 2928,
("Korea", "GV80"): 4063, ("Korea", "G80 (RG3)"): 889, ("Korea", "G70"): 1889, ("Korea", "G90"): 406
}
# 수요량
demand = {
("시카고", "Elantra"): 10719, ("시카고", "Sonata"): 7576, ("시카고", "Kona"): 17659, ("시카고", "G90"): 262, ("시카고", "Venue"): 4008,
("LA", "Sonata"): 4642, ("LA", "G70"): 1050, ("LA", "Venue"): 2900, ("LA", "Kona"): 12209, ("LA", "Tucson"): 30908, ("LA", "GV70"): 2673,
("워싱턴 DC", "Sonata"): 714, ("워싱턴 DC", "Kona"): 9767, ("워싱턴 DC", "Santa Cruz"): 4818, ("워싱턴 DC", "Nexo"): 36, ("워싱턴 DC", "IONIQ 5"): 6134, ("워싱턴 DC", "Santa-Fe"): 15658, ("워싱턴 DC", "Palisade"): 15098, ("워싱턴 DC", "GV60"): 346,
("미시간", "Sonata"): 1330, ("미시간", "G70"): 2104, ("미시간", "G90"): 350, ("미시간", "IONIQ 5 Robo Taxi"): 18, ("미시간", "Santa-Fe"): 14609, ("미시간", "Palisade"): 10860, ("미시간", "GV60"): 643, ("미시간", "GV70"): 1704,
("뉴욕", "Sonata"): 6690, ("뉴욕", "G70"): 1504, ("뉴욕", "Nexo"): 34, ("뉴욕", "IONIQ 6"): 2143, ("뉴욕", "GV70"): 2104, ("뉴욕", "GV70 EV"): 1526, ("뉴욕", "GV80"): 2555,
("캘리포니아", "Elantra"): 13837, ("캘리포니아", "G80 (RG3 EV)"): 124, ("캘리포니아", "Tucson"): 22374, ("캘리포니아", "IONIQ 5"): 8821, ("캘리포니아", "IONIQ 6"): 2123, ("캘리포니아", "GV70"): 1824,
("몬타나", "Elantra"): 17461, ("몬타나", "Sonata"): 3145, ("몬타나", "G80 (RG3)"): 714, ("몬타나", "Tucson"): 10568, ("몬타나", "Santa Cruz"): 4474, ("몬타나", "IONIQ 6"): 1732, ("몬타나", "Palisade"): 7523, ("몬타나", "GV80"): 1912,
("플로리다", "Elantra"): 8256, ("플로리다", "Sonata"): 1115, ("플로리다", "G80 (RG3)"): 963, ("플로리다", "Venue"): 3919, ("플로리다", "Tucson"): 14715, ("플로리다", "Santa Cruz"): 5684, ("플로리다", "Santa-Fe"): 16552, ("플로리다", "Palisade"): 11063, ("플로리다", "GV80"): 3844
}
# 공급량 데이터를 데이터프레임으로 변환
supply_list = [(factory, model, quantity) for (factory, model), quantity in supply.items()]
supply_df = pd.DataFrame(supply_list, columns=["생산공장", "Model", "공급량"])
# 수요량 데이터를 데이터프레임으로 변환
demand_list = [(location, model, quantity) for (location, model), quantity in demand.items()]
demand_df = pd.DataFrame(demand_list, columns=["수요지", "Model", "수요량"])
# 고유한 Model
unique_models=['Elantra',
'Sonata',
'Palisade',
'Kona',
'Venue',
'Nexo',
'Santa Cruz',
'IONIQ 5',
'IONIQ 6',
'IONIQ 5 Robo Taxi',
'Tucson',
'Santa-Fe',
'GV70',
'GV70 EV',
'GV60',
'GV80',
'G70',
'G80 (RG3)',
'G80 (RG3 EV)',
'G90']
1-3. 최적 값을 구하기:
입력한 공급량과 수요량, 단위km당 수송비용을 linprog를 통해서 최소 수송비용을 계산하고, 해당 차량에 대한 판매비용과 순수익률을 바탕으로 최대 순이익을 도출
# 최적화 함수 정의
def optimize_transportation(model):
# 특정 모델에 대해 생산공장 및 수요지 필터링
model_supply_df = supply_df[supply_df['Model'] == model]
model_demand_df = demand_df[demand_df['Model'] == model]
num_supply = len(model_supply_df)
num_demand = len(model_demand_df)
# 비용 벡터 생성
c = factory_to_demand_cost_df.loc[model_supply_df['생산공장'], model_demand_df['수요지']].values.flatten()
# 제약 조건 생성
A_eq = []
b_eq = []
# 공급지에서 수요지로 가는 제약 조건 (공급량)
for supply_idx in range(num_supply):
row = [0] * (num_supply * num_demand)
for demand_idx in range(num_demand):
row[supply_idx * num_demand + demand_idx] = 1
A_eq.append(row)
b_eq.append(model_supply_df['공급량'].iloc[supply_idx])
# 수요지에서 수요량을 충족하는 제약 조건
for demand_idx in range(num_demand):
row = [0] * (num_supply * num_demand)
for supply_idx in range(num_supply):
row[supply_idx * num_demand + demand_idx] = 1
A_eq.append(row)
b_eq.append(model_demand_df['수요량'].iloc[demand_idx])
A_eq = np.array(A_eq)
b_eq = np.array(b_eq)
# 경계 조건 설정
bounds = [(0, None) for _ in range(len(c))]
# 선형 계획법 문제 풀기
res = linprog(c, A_eq=A_eq, b_eq=b_eq, bounds=bounds, method='highs')
# 결과 출력 및 총 비용 계산
if res.success:
print(f"모델 {model}의 최적해를 찾았습니다.")
print(f"모델 {model}의 목적 함수 값:", res.fun)
# 최적해 출력
x = res.x.reshape((num_supply, num_demand))
solution_df = pd.DataFrame(x, index=model_supply_df['생산공장'], columns=model_demand_df['수요지'])
# 전체 위치를 포함한 데이터프레임 생성
full_solution_df = pd.DataFrame(0, index=supply_df['생산공장'].unique(), columns=demand_df['수요지'].unique())
for supply in model_supply_df['생산공장']:
for demand in model_demand_df['수요지']:
full_solution_df.loc[supply, demand] = solution_df.loc[supply, demand]
# 총 공급량 및 총 수요량 추가
full_solution_df["생산량"] = full_solution_df.sum(axis=1)
total_demand = full_solution_df.sum(axis=0)
total_demand.name = "수요량"
full_solution_df = pd.concat([full_solution_df, total_demand.to_frame().T])
print("\n최적해 (공장에서 수요지로의 수송량):")
print(full_solution_df)
# 총 생산대수
total_production = full_solution_df["생산량"].loc["수요량"]
# 결과 저장
results.append([model, total_production, res.fun])
return res.fun, full_solution_df
else:
print(f"모델 {model}의 최적해를 찾지 못했습니다.")
return None
# 특정 모델 최적화 실행 예제
model_name = "Elantra"
optimize_transportation(model_name)모델 Elantra의 최적해를 찾았습니다.
모델 Elantra의 목적 함수 값: 34361796.945362896
최적해 (공장에서 수요지로의 수송량):
시카고 LA 워싱턴 DC 미시간 뉴욕 캘리포니아 몬타나 플로리다 생산량
HMI 0 0 0 0 0 5539 17461 0 23000
HAOS 0 0 0 0 0 0 0 0 0
BHMC 0 0 0 0 0 0 0 0 0
HMMA 0 0 0 0 0 0 0 0 0
HMMC 10719 0 0 0 0 8298 0 8256 27273
HMB 0 0 0 0 0 0 0 0 0
HMMI 0 0 0 0 0 0 0 0 0
HTBC 0 0 0 0 0 0 0 0 0
Vietnam 0 0 0 0 0 0 0 0 0
Korea 0 0 0 0 0 0 0 0 0
수요량 10719 0 0 0 0 13837 17461 8256 50273각 생산지에서 공장까지 배치를 계산
# 전체 모델에 대한 최적화 실행 및 출력
results = []
for model in unique_models:
print(f"모델: {model}")
optimize_transportation(model)
print("\n" + "="*50 + "\n")
# 결과 데이터프레임 생성
results_df = pd.DataFrame(results, columns=["Model", "생산대수", "Minimized Cost: Z"])
# 결과 데이터프레임 출력
print("최적화 결과 데이터프레임:")
print(results_df)최적화 결과 데이터프레임:
Model 생산대수 Minimized Cost: Z
0 Elantra 50273 3.436180e+07
1 Sonata 25212 1.952205e+07
2 Palisade 44544 3.125782e+07
3 Kona 39635 2.248018e+07
4 Venue 10827 7.865329e+06
5 Nexo 70 3.108921e+04
6 Santa Cruz 14976 1.190703e+07
7 IONIQ 5 14955 9.780904e+06
8 IONIQ 6 5998 3.850152e+06
9 IONIQ 5 Robo Taxi 18 1.557806e+04
10 Tucson 78565 3.998219e+07
11 Santa-Fe 46819 3.049194e+07
12 GV70 8305 2.715508e+06
13 GV70 EV 1526 3.298023e+05
14 GV60 989 5.312487e+05
15 GV80 8311 4.355275e+06
16 G70 4658 3.168376e+06
17 G80 (RG3) 1677 1.169699e+06
18 G80 (RG3 EV) 124 8.069883e+04
19 G90 612 4.833041e+05# 판매 데이터 (제공 데이터셋 기반)
sales_data = {
"Model": ["Elantra", "Sonata", "Palisade", "Kona", "Venue", "Nexo", "Santa Cruz", "IONIQ 5", "IONIQ 6",
"IONIQ 5 Robo Taxi", "Tucson", "Santa-Fe", "GV70", "GV70 EV", "GV60", "GV80", "G70",
"G80 (RG3)", "G80 (RG3 EV)", "G90"],
"판매 가격 (USD)": [20000, 25000, 35000, 30000, 20000, 60000, 28000, 45000, 47000, 55000, 27000, 32000,
50000, 65000, 60000, 70000, 45000, 50000, 70000, 80000],
"순이익율 (%)": [5, 6, 10, 10, 5, 10, 7, 12, 12, 12, 6, 7, 12, 15, 15, 12, 10, 10, 15, 12],
"전기차 유무": ["X", "X", "X", "O", "X", "O", "X", "O", "O", "O", "X", "X", "X", "O", "O", "X", "X", "X", "O", "X"]
}
sales_df = pd.DataFrame(sales_data)
# 1대당 순이익 계산
sales_df["1대당 순이익"] = sales_df["판매 가격 (USD)"] * (sales_df["순이익율 (%)"] / 100)
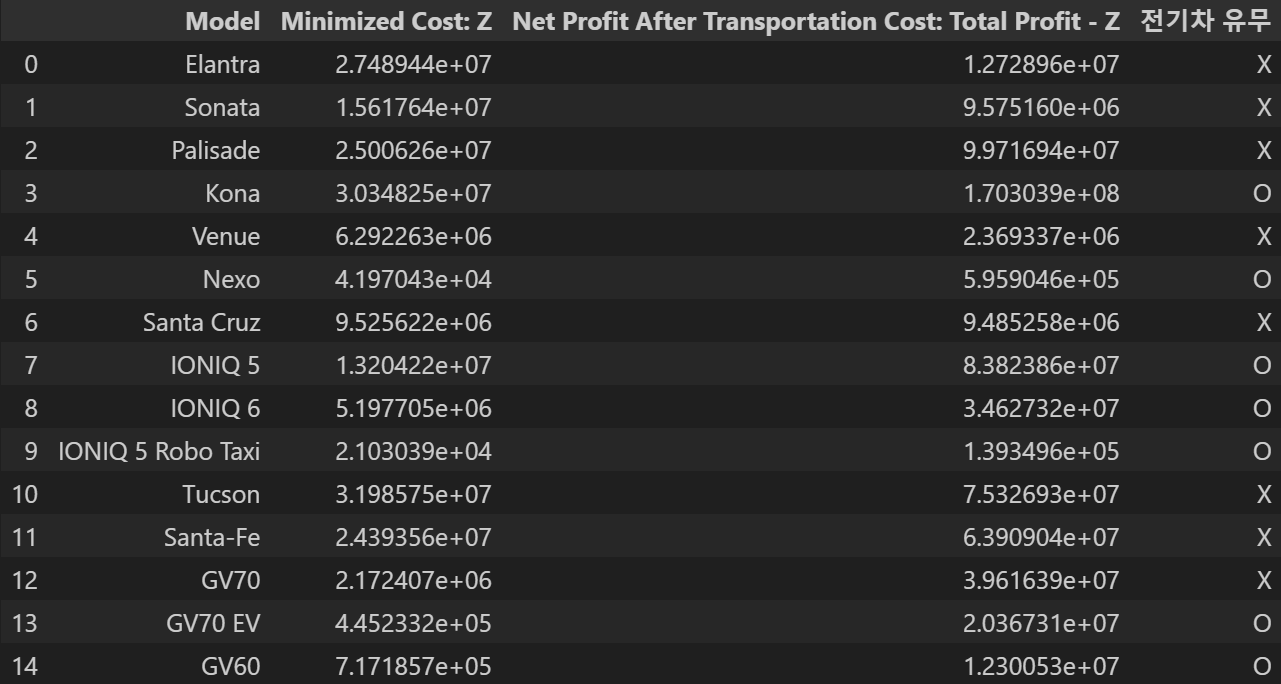
# 판매 데이터와 최적화 결과 데이터 병합
merged_df = pd.merge(results_df, sales_df, on="Model")
# 총 이익 계산
merged_df["profit"] = merged_df["생산대수"] * merged_df["1대당 순이익"]
# 순이익에서 운송 비용을 뺀 값 계산
merged_df["Net Profit After Transportation Cost: Total Profit - Z"] = merged_df["profit"] - merged_df["Minimized Cost: Z"]
# 병합된 데이터프레임 출력
print("병합된 데이터프레임:")
merged_df
2. 민주당 당선시의 시나리오
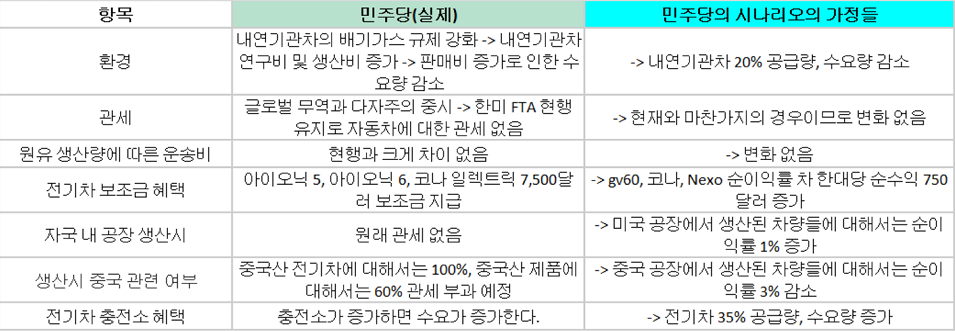
데이터셋의 수정만 있을 뿐 방법은 위의 기본문제와 같으므로 코드를 살짝만 수정한다.
# 공급량 조정
supply_df.loc[supply_df['Model'].isin(내연기관차), '공급량'] *= 0.8
supply_df.loc[supply_df['Model'].isin(전기차), '공급량'] *= 1.35
# 수요량 조정
demand_df.loc[demand_df['Model'].isin(내연기관차), '수요량'] *= 0.8
demand_df.loc[demand_df['Model'].isin(전기차), '수요량'] *= 1.35# 순이익율 조정
def adjust_profit_margin(row):
if row["생산공장"] == "BHMC_HTBC":
return row["순이익율 (%)"] - 3
elif row["생산공장"] == "HMMA":
return row["순이익율 (%)"] + 1
else:
return row["순이익율 (%)"]
merged_df["조정된 순이익율 (%)"] = merged_df.apply(adjust_profit_margin, axis=1)
3. 공화당 당선시의 시나리오
마찬가지로 과정은 비슷하지만 이번에는 육, 해상의 수송비용 또한 변화하였다.
# 공급지에서 미국 항구로 가는 거리 및 비용 계산
supply_to_port_cost = np.zeros((len(supply_df), len(port_df)))
for i, supply in supply_df.iterrows():
for j, port in port_df.iterrows():
distance = haversine((supply['위도'], supply['경도']), (port['위도'], port['경도']), unit=Unit.KILOMETERS)
cost = 0.04 * distance #수정된 해상비용
supply_to_port_cost[i, j] = cost
supply_to_port_cost_df = pd.DataFrame(supply_to_port_cost, index=supply_df['생산 공장'], columns=port_df['미국 항구'])
# 미국 항구에서 수요지로 가는 거리 및 비용 계산
port_to_demand_cost = np.zeros((len(port_df), len(demand_df)))
for i, port in port_df.iterrows():
for j, demand in demand_df.iterrows():
distance = haversine((port['위도'], port['경도']), (demand['위도'], demand['경도']), unit=Unit.KILOMETERS)
cost = 0.1 * distance #수정된 육상비용
port_to_demand_cost[i, j] = cost
port_to_demand_cost_df = pd.DataFrame(port_to_demand_cost, index=port_df['미국 항구'], columns=demand_df['수요지'])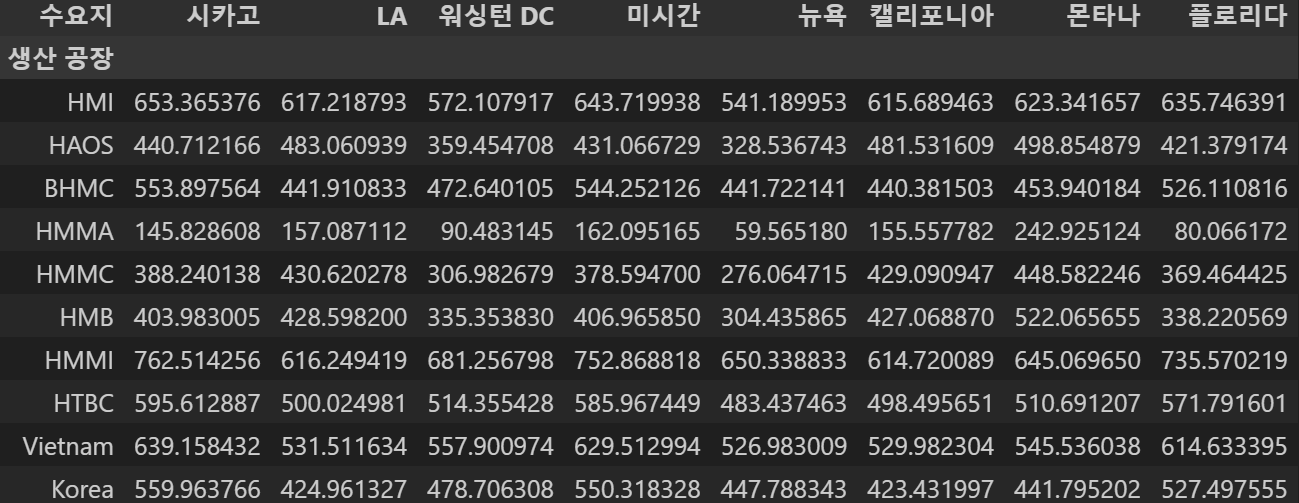
# 공급량 조정
supply_df.loc[supply_df['Model'].isin(내연기관차), '공급량'] *= 1.3
supply_df.loc[supply_df['Model'].isin(전기차), '공급량'] *= 0.9
# 수요량 조정
demand_df.loc[demand_df['Model'].isin(내연기관차), '수요량'] *= 1.3
demand_df.loc[demand_df['Model'].isin(전기차), '수요량'] *= 0.9# 순이익율 조정
def adjust_profit_margin(row):
if row["생산공장"] == "BHMC_HTBC":
return row["순이익율 (%)"] - 3
elif row["생산공장"] == "HMMA":
return row["순이익율 (%)"] + 2
else:
return row["순이익율 (%)"]
merged_df["조정된 순이익율 (%)"] = merged_df.apply(adjust_profit_margin, axis=1)
3개의 조건을 모두 계산했을 때의 순이익의 합을 계산해 보면
기본문제: 705919767.069407
민주당 시나리오: 708168943.363676
공화당 시나리오: 905493930.526807
약 2억 달러 차이로 공화당 당선 시 현대차가 이득이라는 결과가 나왔다.
본인이 생각한 이유로는 공화당 당선 시 전기차의 공급, 수요량이 10퍼센트밖에 줄지 않은 반면, 오일에너지 정책으로 인해서 수송비용이 크게 감소했고, 안 그래도 많은 비중을 차지하고 있는 내연기관 차에 공급, 수요량을 30퍼센트나 증가한 게 그 이유가 아닐까 싶다.
민주당 당선 시에도 전기차 수요공급이 35퍼센트이지만 그만큼 내연기관이 20퍼센트 감소하여 기본문제와 큰 차이점이 없다는 것도 확인 가능하다.
현실적으로 대선 결과에 따라서 30% 근처의 수요 급증, 급감 이 가능하냐는 의문이 들었지만...
(실제로 심사관들 또한 의문을 가졌었음)
문제를 위해 주어진 조건이므로 넘어간다.
2-2 TASK2: TASK1의 대선결과를 뒤집는 조건을 임의로 추가하여 새로운 기업 순이익 계산
조건: 기존과 다른 조건 추가를 통해서 TASK1의 결과를 뒤집는 결과 도출하기
Task1에서 공화당의 당선이 현대차에게 2억 달러의 차이로 이득을 주는 것을 확인했으니 이번에는 새로운 조건을 추가하여 민주당이 당선되었을 때 현대차에게 더 큰 이익을 가져올 수 있도록 만들어야 한다.
문제 조건 중에 민주당, 공화당 시나리오의 조건과 비슷하면 안 된다는 추가 제한이 들어왔다. 아무래도 그냥 단순하게 순이익 % 몇 개만 조정하면 손쉽게 민주당이 이기는 결과를 얻을 수 있어서 그런 것 같다.
우리 조는 그래도 공약에 포커스를 맞춰서 조건을 내려고 했다. 이미 공장 가동을 앞두고 있는 메타플랜트 아메리카를 조건에 넣고 싶었지만, 해당 공장은 대선결과 여부에 관계없이 10월에 가동 예정인 관계로 조건 추가를 하지 않았다.
(근데 다른 조는 조건으로 추가했다)

여기에서 우리 조가 당면한 문제가 생긴다.
순이익률과 수요, 공급량을 마음대로 정해도 되는 건가? 에 대한 의문이 계속해서 나왔다.
결론적으로는 주어진 조건들 또한 임의로 만든 것이기에(출제자 피셜) 우리 또한 임의로 증가감소량을 정해도 된다는 판단하에 정하기로 했다.
하지만 입상한 조는 어떻게든 근거를 찾으려고 노력했고, 그 과정에서 회기분석 등의 기법을 사용하기도 했다.
조금 억지이긴 해도 그렇게 근거를 찾아서 하는 게 좀 더 설득력 있다고 판단했던 것 같고, 내 생각도 같다.
1. 민주당 새로운 시나리오
# 공급량 조정
supply_df.loc[supply_df['Model'].isin(내연기관차), '공급량'] *= 0.8
supply_df.loc[supply_df['Model'].isin(전기차), '공급량'] *= 1.35*1.15
# 수요량 조정
demand_df.loc[demand_df['Model'].isin(내연기관차), '수요량'] *= 0.8
demand_df.loc[demand_df['Model'].isin(전기차), '수요량'] *= 1.35*1.15# 순이익율 조정 함수
def adjust_profit_margin(row):
adjusted_margin = row["순이익율 (%)"]
if row["Model"] in electric_models:
adjusted_margin += 4
if row["생산공장"] == "BHMC_HTBC":
adjusted_margin -= 3
elif row["생산공장"] == "HMMA":
adjusted_margin +=1
return adjusted_margin
2. 공화당 새로운 시나리오
# 순이익율 조정 함수
def adjust_profit_margin(row):
adjusted_margin = row["순이익율 (%)"]
if row["Model"] in electric_models:
adjusted_margin -= 3
if row["생산공장"] == "BHMC_HTBC":
adjusted_margin -= 3
elif row["생산공장"] == "HMMA":
adjusted_margin += 2
return adjusted_margin
결과값:
민주당: 900899836.191798
공화당: 842952993.526807
약 6천만 달러 차이로 민주당이 더 높은 순이익을 가져오는 것으로 나온다.
<모든 SESSION2의 계산은 파이썬과 엑셀 모두 사용해 값이 똑같이 나옴을 확인했다>
엑셀로도 위의 계산식들을 모두 풀 수 있다. 기본문제만 예시로 들어본다면,

제공된 데이터셋에서 위, 경도 좌표를 가지고 haversine() 공식을 통해 거리를 구한다.
모든 공급지 -> 수요지의 거리를 계산한 뒤 수송비용을 곱해 최종 수송비용을 구한다.
거기에서 최소인 값들만 고르기 위해 min함수를 사용했다.
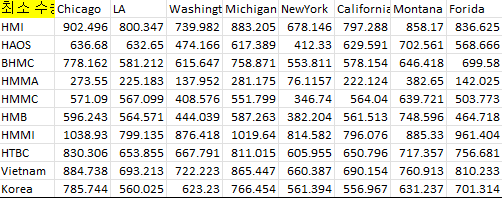

엑셀의 해찾기 기능을 추가하고, 목적함수값 셀을 최소로 하는 LP 계산식을 이용한다.
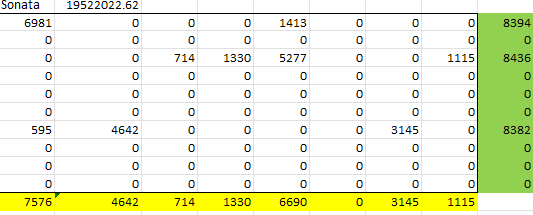
해 찾기를 하게 되면 위와 같이 자동으로 Minimized cost: Z값과 각 공급지와 수요지의 수송표가 나오게 된다.
여기에 각 차량에 따라서 차량의 비용을 곱해 매출을 구하고, 거기에 순수익률을 구하고 수송비용을 빼서 최종 순이익을 구한다.(각 조건에 따라서 공급, 수요량, 순수익률 등을 조정해 준다)
엑셀로 해도 방법만 알면 나름 쉽게 해결이 가능하다. 다만, 조건이 추가될 때 모든 차종을 하나하나 손수 바꿔줘야 한다는 점이 반복된 작업을 하게 만든다.
기억에 남았던 질문:
- 미국에 공장을 설립하는 게 확정적인 수익을 기대하는 것도 아닌데 어떻게 생각하느냐- lg cns
- 당연히 확정적으로 수익을 낼 수 있을 것이라고 생각하지 않는다. 하지만, 미국의 내수화를 진행함에 따라서 대미수출에 상당한 타격을 받을 수 있는 것은 기정사실이라고 생각한다. 대한민국 반도체, 이차전지, 전기차의 상당 부분은 미국수출에 의존하고 있기 때문에 이런 상황에 유연하게 대응해야 한다.
미국 내 공장 증설은 반드시 수익을 보장하는 것은 아니지만, 장기적인 전략과 현지화, 기술 혁신을 통해 리스크를 줄이고 수익성을 확보할 수 있는 방법을 찾을 수 있는 방법 중에 하나이다. 이를 위해서는 정책 변화에 대한 민첩한 대응, 자동화 기술의 적극적인 도입, 현지화 전략의 강화가 중요하다.
- 민주당과 공화당의 당선에 따른 정확한 영향의 차이를 모르겠다.
- 사실이다. 당선공약을 보면 서로 닮은 부분이 있는 것이 확인된다. 에너지 중점 같은 핵심적인 공약들은 극명하게 나뉘지만, 반도체 같은 첨단 기술들은 두 당 모두 미국 내수화를 진행하기 때문에 비슷한 결과가 나올 수 있다.
이차전지나 전기차의 경우는 극명하지는 않지만 비슷한 부분이 많이 보이는 것 같다.
내가 생각하는 탈락요인:
일단 가장 큰 요인은 파일을 잘못 보낸 것이다. 본인과 다른 팀원들이 계산한 값을 잘 정리해 달라 했고, 제출할 때 그분이 압축을 해서 줘 다른 팀원들은 파일의 내용을 확인하지 못했다. 미리 대비하여 한번쯤은 검수를 해야 했으나 너무나 촉박해 확인하지 못했다.(나중에 스태프였던 친구에게 들었더니 모든 문제의 정답을 기본문제 정답이랑 같이 냈다고 했었다)
두 번째는 좀 더 일찍 시작하지 않았다는 것이다. 필드캠프 하기 전 일주일이란 시간이 있었지만, SESSION1 에만 너무 집중하여 일주일을 해당 문제에 대한 조사만 진행했었다. 부랴부랴 SESSION2 Task 1 까지는 전날에 다 했지만, 캠프 당일날 생각보다 적은 준비시간에 상당히 촉박했다. 좀 더 힘들게 준비했어야 캠프 당일날에 여유가 있을 것 같다.
(실제로 어떤 조는 12시에 최종파일 제출하고 발표준비를 한 조도 있었다)
세 번째는 결국 시간과 관련되어 SESSION2 Task2 할 때 적절한 근거를 찾지 못했다는 것이다. 또한 Task2를 할때 상당시간을 그냥 날렸는데, 그 이유는 새로운 조건을 만들 때 이게 과연 새로운 조건인가, 공약과 관련이 있는가 등에 대한 의문점이 계속 들어 아이디어가 떠올라도 무산됐던 것들이 많았다. 너무 어렵게 생각해서 끝내는데 어려웠던 것이 아닌가 싶다.
결국은 시간싸움에서, 우리 조는 시간을 허비한 감이 있었던 것 같다. 팀원과 의견이 맞지 않을 때마다 중재하며 대안점을 찾았지만, 제한된 시간 내에서 의견의 갈등 발생은 상당한 시간을 끌었다.
다음에 또 참여한다면, 일단 좀 서둘러 준비하고, 생각보다 꼼꼼하게 근거를 찾고, 제출기한을 여유롭게 남겨 제출 파일이 정확한 것인지 파악이 가능하도록 해야겠다.
여담이지만 파일 잘못 낸 사실은 나밖에 모른다. 좋게 끝난 분위기를 굳이 망치고 싶지는 않아서...(그분은 아직도 모르겠지)
끝!
'대외활동' 카테고리의 다른 글
| 수원시 유동인구데이터 기반 데이터 흡연구역 설치 (5) | 2024.12.24 |
|---|---|
| 고용노동 공공데이터 공모전 기록- 라이터서비스 (5) | 2024.09.03 |